当前位置:首页 » 国际化教育理念 » 正文
-
今天的文章我想分享给家长们两个小问题,以测试孩子对所学知识的理解程度。
01 时间问题
我记得以前小学陪妈妈去买菜的时候,街市里面称重量的时候,用的是多少斤,多少两或者多少磅。
我小时候也会常常叫妈妈经常量一下我的高度,用的是多少尺多少寸,例如我现在便是六呎一吋高。
直到上了小学之后,我开始接触到另一种测量的方法。
重量方面,我学到了一公斤(1kg)等于一千克(1000g)。
长度方面,我学到了一厘米(1cm)等于十毫米(10mm),一米(1m)等于一百厘米(100cm),一公里(1km)等于一千米(1000m)。
当时的小学老师解释,这一种制度叫做”十进制“。
采用”十进制的好处便是把整个制度简单化,方便量度和理解。
这样的话并不需要紧记一尺等于多少寸,一斤等于有多少两,一磅有多少安士等等。
这个时候,我的同学Joyce便举手问了一个问题。
“既然十进制这么好用的话,为什么1小时不是100分钟?1分钟不是100秒?”
孩子们有没有想过这个问题?
或者我应该问,家长们以前读书的时候有没有想过这个问题?
这里当中牵涉的知识其实只是小学程度而已,关键在于我们学数学的时候,是否着重理解,学得是否够深入,还是只是停留于做题目的阶段。
答案我会在文章末段揭晓。
02 勾股定理

勾股定理是中学阶段的必学知识点,公式是
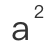 +
+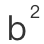 =
=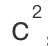 。
。大约在一个多月之前,我在课堂上向已学过勾股定理的学生问了以下两个问题:
1、“为什么勾股定理当中用的是
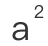 ,
,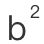 和
和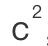 ?为什么不是
?为什么不是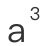 ,
,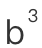 和
和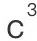 ,甚至
,甚至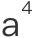 ,
,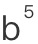 和
和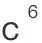 ?”
?” 2、“为什么是
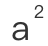 +
+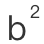 =
=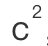 ?为什么不可以是减数,乘数或者除数?为什么一定要相加?”
?为什么不可以是减数,乘数或者除数?为什么一定要相加?” 全班鸦雀无声,整个课堂仿佛静止了30秒......
接着我对他们说了以下这一段说话:
你们利用勾股定理公式把所有题目做对了,的确是不错。按道理来说,我应该很开心。但你们犯了一个学生们普遍会犯的错误,就是读死书。
能够正确地运用勾股定理去做题目,拿高分,但你们根本并不透彻了解勾股定理。
从分数上来说,你们是成功了。从理解上来说,你们是失败了。
你们毕业以后出来社会工作,你觉得工作上能够用到勾股定理的机会有多大?
你认为会有客户走过来给你一条勾股定理的问题,然后要你去解题吗?
数学中的勾股定理只是一个工具,重要的并不是工具本身,而是透过工具学习到的理解能力,推理能力和逻辑思维的能力。
这一种能力才能够让你在毕业之后运用在不同的行业当中,不同的岗位当中,这样的话,我教你们数学才有意义。
作为老师,我可能有一点唠叨,但看着一班聪明的学生深陷于读死书的漩涡之中,我认为必须有义务把他们拯救出来。
教育必须面向未来,不能只顾现在。
如果由我来教勾股定理的话,我甚至根本不会把这条公式告诉学生。
而是给他们很多直角三角形,叫他们用间尺自己去探索一下,看一下能否找出a2+b2=c2这种关系。
如果他们找不到的话,我才逐渐地给予他们一步一步的引导,最终还是希望他们能够把这条理论自己推理出来。
我的教育理念是:
如果学生是真正透彻了解数学理论的话,他们自然就会懂得做题目,高分自然就会来。
目的地其实是一样的,只是我选择了一条虽然长,但是更有发掘力的路去走。
03 融会贯通
回到之前的那道问题:
既然十进制那么好,为什么1小时不是100分钟?1分钟不是100秒?
其实背后的理论就是小学程度的因子(Factor)。
因子就是一个合数分解成的那些质数。比如说15的因子就是1, 3 ,5, 15。
如果要令时间更加实用和好用的话,它们必须很容易地分成很多小段。
例如,5分钟,15分钟,20分钟等等,因此必须用到因子这个理论。
从因子的角度去看,12会比10更好。
10的因子只有1,2,5,10,但12的因子有1,2,3,4,6,12。
但12这个数字也覆盖不了5和10这两个数字,因此最好的办法就是把10和12合并起来。
而10和12的最小公倍数就是60。
因此60其实是一个非常神奇的数字,因为它有非常多的因子,甚至很多比60大的数字因子都没有60的多。
60的因子有1,2,3,4,5,6,10,12, 15,20,30,60。
这样的话,时间便可以很方便地分成很多小,实用性便会大大提高。
这就是当初巴比伦人为什么采用六十进制的原因。
它和十进制的理论是截然不同的。
但学生必须要对所有知识点融会贯通才知道什么时候应该采用怎样的理论去解决问题。
这就好像打羽毛球时,什么时候应该用正手打,什么时候应该用反手打。
如果你球技高的话,球一来到的时候,便已经知道了应该用什么方法去打这个球是最好的。
这就是把知识融会贯通的意思。
04 寻根究底
现在回到勾股定理的问题。要解答之前我的两道问题只需要一幅图。
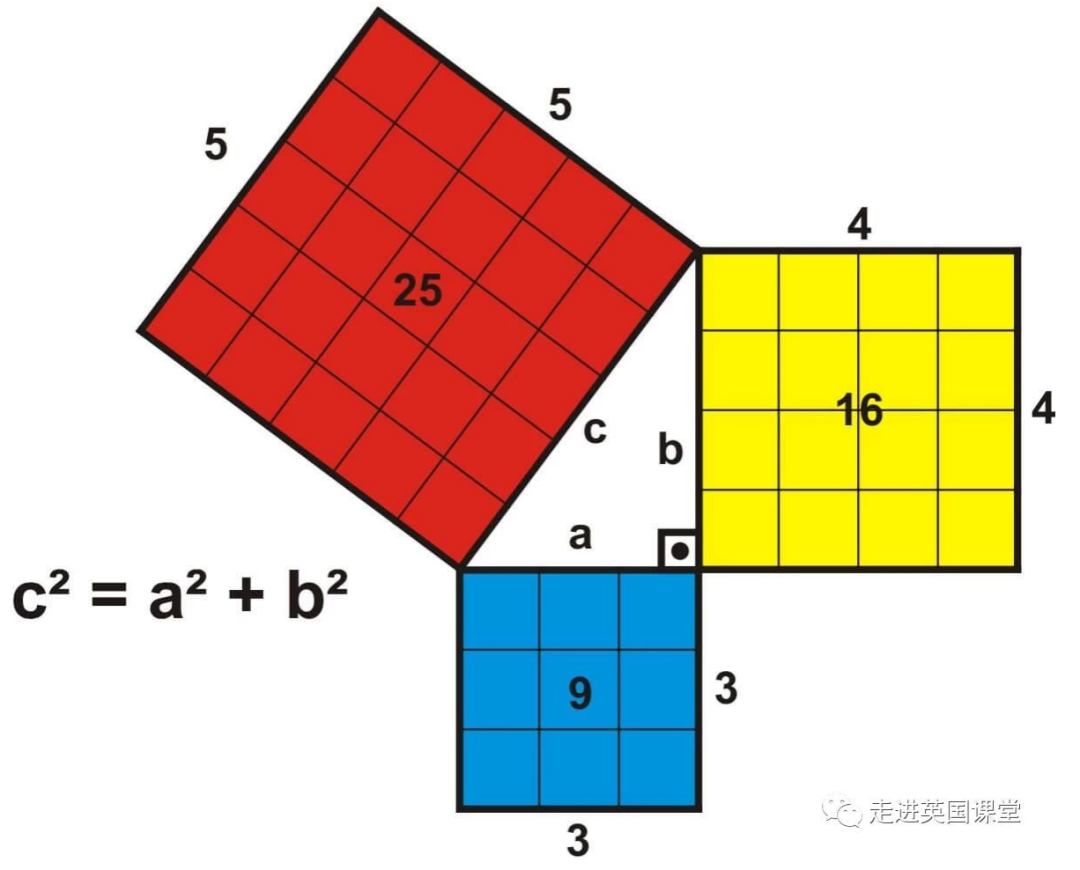
第一道问题的答案就是:
因为勾股定理,意思其实是每一边形成一个正方形,要计算正方形的面积的话就必须要用
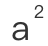 ,
,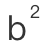 和
和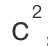 ,因此不会用
,因此不会用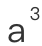 ,
,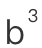 和
和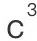 ,甚至
,甚至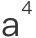 ,
,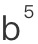 和
和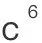 。
。第二道问题的答案,与第一道相关联,因为勾股定理的意思是,两个小的正方形的面积的总和,就会是等于大的正方形的面积。
这就解释了为什么不能用减数,乘数或者除数。
很多学生只知道了结果,但并不知道原因。
当然,这只是理解勾股定理的方法,而并不是证明勾股定理的办法。
有很多学生到了这一步其实还没有完全明白,这个时候便需要用片段来解释。
每一次教勾股定理的时候,我都会在youtube找一条片段放给学生看,片段的名字叫:pythagoras water。
影片一开始的时候有两个小的正方形里面充满了水,然后盘子便会开始倒过来。

这个时候水会由两个小的正方形,流到大的正方形内。

最后,两个小正方形加起来的水刚好填满了一个大的正方形。

以我的教学经验,没有一名学生在看过这一段影片之后还不明白勾股定理的。
05 结语
你可能认为,孩子会否读死书要视乎他们碰上了怎样的老师,如何去引导他们,是否只满足于分数而已。
我并不同意这种说法。
我认为读死书其实是一种选择,一种是否愿意动脑筋去思考问题的选择。
但我绝对不能否认,一名好老师对于孩子是否能够达到优秀的程度,起着十分重要的作用。
教师不能把学生教成一个活动的书橱,而是要教学生如何思考。
本篇文章来源于微信公众号: Miki粥
推荐阅读:
版权声明:“备战深国交网”除发布相关深国交原创文章内容外,致力于分享国际生优秀学习干货文章。如涉及版权问题,敬请原作者原谅,并联系微信547840900(备战深国交)进行处理。另外,备考深国交,了解深国交及计划参与深国交项目合作均可添加QQ/微信:547840900(加好友时请标明身份否则极有可能加不上),转载请保留出处和链接!
非常欢迎品牌的推广以及战略合作,请将您的合作方案发邮件至v@scieok.cn本文链接:http://scieok.cn/post/2473.html
-
<< 上一篇 下一篇 >>
教育只看分的家长输了!两个问题测出小孩是不是“死读书”。
15886 人参与 2021年10月31日 16:01 分类 : 国际化教育理念 评论
search zhannei
深国交2024年英美本科录取小计
-

未标注”原创“的文章均转载自于网络上公开信息,原创不易,转载请标明出处
深国交备考 |
如何备考深国交 |
深国交考试 |
深国交培训机构 |
备战深国交 |
联系方式
Copyright www.ScieOk.cn Some Rights Reserved.网站备案号:京ICP备19023092号-1商务合作
友情链接:X-Rights.org |中国校园反性骚扰组织 | 留学百词斩 | 南非好望角芦荟胶 | 云南教师招聘考试网 | 备战韦尔斯利网| 备战Wellesley



